Return to MODULE PAGE
Building a Machine that Can See
David Leech Anderson: Author
Perception is one area of inquiry in cognitive science. Perception is the process(es) whereby we obtain information about the world. For example, we interact with other people, animals and things based on information from sight, hearing, touch, or smell. Perception is so effortless, seemingly instantaneous, and apparently reliable that it is difficult to appreciate that it is, in fact, exceeding complex, requires measurable time, and fallible. Unlike other information processing, perceptual processes are so inaccessible to the conscious mind that people have little intuitive understanding of it. One way to gain an appreciation of the problems in understanding perception is to consider how one would build an artificial system which would do at least some of what the natural system does.
 Consider the following
problem in machine-vision:
Consider the following
problem in machine-vision:
Build a machine to negotiate unknown terrain without a human operator
The first problem we encounter is how to provide our machine with information about the terrain. What kind of device should we provide our machine to receive information from the world?
Image formation
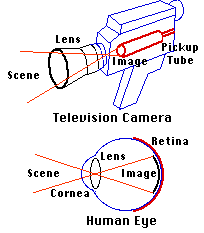 Suppose we choose a television camera to provide continuous
information about the terrain. Light reflected from the terrain is focused by
optical elements on a photosensitive surface of the pickup tube, much like the
lens of the human eye focuses light on the retina, to form an image of the scene.
But television cameras are not perfect instruments. Background electromagnetic
radiation produces "ghost" images. Optical elements in the camera produce distortions
such as blurring and curved lines. Such distortions are particular large for
the human optical pickup we call the eye. We require a higher-quality camera
for our machine. But there are other problems.
Suppose we choose a television camera to provide continuous
information about the terrain. Light reflected from the terrain is focused by
optical elements on a photosensitive surface of the pickup tube, much like the
lens of the human eye focuses light on the retina, to form an image of the scene.
But television cameras are not perfect instruments. Background electromagnetic
radiation produces "ghost" images. Optical elements in the camera produce distortions
such as blurring and curved lines. Such distortions are particular large for
the human optical pickup we call the eye. We require a higher-quality camera
for our machine. But there are other problems.
Image processing
A television signal is a numerical coding of the intensity values of light (image) reflected from different places in the terrain.


The intensity of reflected light is different for different reasons: Light intensity will be different across the edges of objects like boulders, but also within objects that have varied texture as boulders often do. Also light intensity will change where there are changes in illumination, as when shadows are cast by a boulder or hole.
We must provide our machine with processes which filter and organize the television input at different size scales to distinguish the edges of objects from their texture. Our machine must also distinguish between changes in reflected light that arise from differences in physical structures and those arising from changes in illumination. Obviously, this is a formidable task.
Researchers in image processing (e.g., Marr, 1982) depend upon knowledge of how images are formed to extract a "picture" of the scene, a high-quality, two-dimensional representation in which the elements are identified by their source (e.g., edges vs. shadows, object vs. background). The human retina and central nervous system perform similar image processing. We will skip over the enormous detail of image processing and assume that our machine is provided with a picture of the terrain, much like our television provides us with pictures. But this is only a good start.
Picture analysis
Now, who sees the picture? Remember, we have no human operator. Our machine must be able to interpret the picture in terms of the physical world. Our machine must, for example, be able to distinguish slopes and obstacles such as holes and boulders. How might our machine do this? What does a slope or a boulder look like? What do we tell our machine to look for in the picture?
Slopes and texture gradients
Slopes might be distinguished by changes in the grain or texture of the picture. If the terrain is made up of objects of uniform size (e.g., pebbles), then a picture of this terrain will be made up of elements graded in size, decreasing with distance.

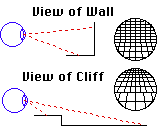 And,
most importantly, changes in slope will be indicated by changes in these gradients.
For instance, a cliff will be marked by an abrupt break in texture gradient
and an upward slope would be signaled by a more gradual decrease in gradient.
And,
most importantly, changes in slope will be indicated by changes in these gradients.
For instance, a cliff will be marked by an abrupt break in texture gradient
and an upward slope would be signaled by a more gradual decrease in gradient.
Our machine might be designed to detect such texture gradients, but it would be "looking" at the relative size of adjacent elements in the picture, not the picture itself. Our machine would be performing an analysis of the picture. Thus, a picture of the scene is only the starting point for perception. Our brain must also perform an analysis of the picture it receives.
Moreover, this texture gradient analysis is possible only if elements in the scene have a uniform size. You see, our machine must have some information about regularities of the physical world in the form of assumptions. In fact, the nature of the physical world is such that surfaces usually are made up of uniform elements. For example, rain, wind, ice, and snow operate to reduce rock to pebbles of usually uniform size, usually but not always. Our machine will sometimes error by making this assumption, but not often, and without some such assumption it cannot even begin to analyze the picture. Also, the human perceptual process is only possible because of similar assumed physical regularities.
Objects and Shadow Formation

What about obstacles like holes and boulders? We would want our machine to distinguish between these two kinds of objects because they require different kinds of locomotion.

Our machine might distinguish such obstacles in the terrain based on the physical fact that shadows fall outside the contour of an elevation and inside the contour of a depression. Again, our machine is performing an analysis of the picture and its ability to do such an analysis depends upon its having information about the physical characteristics of the world.
Of course, this regularity of shadow formation is only available when there are shadows. For cloudy days, we would have to provide our machine with other means of distinguishing obstacles.
Object Size and Rigidity
Given that our machine could distinguish holes and boulders, how might it be able to tell the size of such obstacles? Can it move over a hole or boulder or must it go around? The size of the obstacle in the (motion) picture is no help, because this will change as our machine moves toward or away from the obstacle. Indeed, how can our machine distinguish change in picture element size that arises from change in the distance to the obstacle and change that might arise from changes in size of the obstacle itself? Even if our machine could distinguish when it, itself, were moving, picture element size would still be not be helpful because object size could be changing to compensate for machine movement! If we build into our machine the (usually valid) assumption that objects are rigid, unchanging in size, then it could compute obstacle size by taking distance into account.

Of course, in a watery world where some objects like jellyfish do change size the rigid-world assumption would not work! We would then have to provide our machine with other ways of determining the relationship between sizes of elements in the picture and objects in the terrain. In general, any single assumed physical regularity is valid only in limited circumstances. Many such assumptions are necessary for the picture analysis performed by the human brain.
Object Distance and Motion Parallax
 But, how can
our machine discriminate distance? We might seek a solution to this problem
by employing a powerful source of distance information for the human visual
system: motion parallax. As we move about the world, objects in the picture
our brain receives are displaced by different amounts depending upon their
distance from us and where we are looking.
But, how can
our machine discriminate distance? We might seek a solution to this problem
by employing a powerful source of distance information for the human visual
system: motion parallax. As we move about the world, objects in the picture
our brain receives are displaced by different amounts depending upon their
distance from us and where we are looking.
In general, the farther an object is from us, the less is the displacement. This displacement, however, is cancelled out when we move our eyes to fixate a particular object in the scene. The sum of body and eye movement vectors produces gradients of increasingly greater displacement, opposite the direction of our movement for objects nearer than the fixation point and in the same direction as our movement for object farther than the fixation point.
These gradients of displacement correlate well with distance, but this relationship is only valid because we assume that the world itself is not moving! The assumption of a stable world is so strong that when it is violated as in an earthquake, we find it very distressing. This assumption can even make us feel like we are moving as we sometimes do in a parking lot when the car next to us starts to move.
We could provide our machine with a scale that relates the motion parallax gradient to distance. But again, notice that our machine is performing an analysis of the picture, looking for displacement of a picture element in order to compute distance to that object in the world. Our machine's television picture is only the starting point for its perceptual process. So too, the picture our brain receives is only the beginning of our perception of the world. Perception is an process of analysis, not picture collection!
Topic for Further Study: What if we were to provide our machine with two cameras, giving it binocular vision like humans (an animals)? What problems would such stereoscopic vision solve? What are the limitations of stereoscopic vision? (see Coren & Ward, 1989, for further information)
Summary
Notice that our machine is getting increasingly complex in process and
in the information it must have to carry out that processing. Slope perception
depends upon processing texture gradients which is possible only if we
assume the elements have a uniform size. Distinguishing between obstacles
like holes and boulders depends upon information about of how shadows
are formed. Size perception requires first fixing the relationship between
sizes of picture elements and objects in the world, which depends upon
the assumption of rigid objects, and then computing distance from the
motion parallax gradient which itself depends upon the assumption of a
stable world. Once our machine determines the size that an object has
in its television picture and the distance to the object, the size of
the object itself can be calculated from the physical law that picture
size is inversely related to distance. We would also have to provide our
machine with this physical law of the visual angle.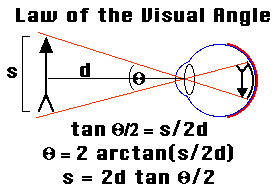
So, our machine will have two kinds of information built into it: laws and assumptions. Laws are (presumably) universals, but assumptions are only regularities. A law is always true, but an assumption is only true sometimes, perhaps most of the time, but only in limited circumstances. Laws produce one interpretation; assumptions only reduce the number of possible interpretations. A single assumption constrains interpretation, but does not produce a single interpretation. In our machine and in the human perceptual system, many assumptions working together with a few laws can constrain perception to a single interpretation of the world.
Basic theoretical problem
This exercise in designing a seeing machine illustrates the basic theoretical problem of perceptual science: Given the information available in a physical image, what are the minimal processes and assumptions necessary to produce accurate perception? Such perception is not simple snapshot collection. It requires analysis of a picture to extract critical information and interpretation of that information in light of information about regularities in the world (i.e., laws and assumptions). Only in this way do we arrive at veridical perception, perception which corresponds to the scene.
Conclusions
The understanding of human perception can be viewed as analogous to the problem designing our machine, but in the reverse direction. We start with a functioning system and we must understand how it does what it does. Such reverse engineering is a multidisciplinary enterprise because the perceptual system is a part of the world. It evolved in the world and has incorporated detailed information about that world. Physics, biology, and computational science, as well as psychology, are necessary to understanding the physical laws and regularities that make the perceptual process possible.
Topic for Further Study: What about the other perceptual modalities? How does the present analysis of vision apply to hearing, touch, and smell? (see Coren & Ward, 1989, for further information)
Bibliography
Coren, S., & Ward, L. M. (1989). Sensation and Perception, 3rd Ed. New York: Harcourt Brace Jovanovich.
Marr, D. (1982). Vision: A Computational Investigation into the Human Representation and Processing of visual information. San Francisco: Freeman.
Stillings, N. A., Weisler, S. E., Chase, C. H., Feinstein, M., Garfield, J. J., & Rissland, E. L. (1995). Cognitive Science: An Introduction, 2nd Ed. Cambridge, MA: MIT Press.



