Return to MODULE PAGE
Introduction to Visual Illusions
Gordon Redding: Author
An experiment was done to determine how subjects respond to visual stimuli (in this case, line drawings) that produce visual illusions (Müller-Lyer illusions). Before examining the details of the experiment, it is important to understand some of the basics about illusions.
Visual systems are typically adapted to the physical regularities in their environment. This is true whether it is a natural system (like humans) or an artificial system (like robots). The system must take account of the laws of physics, for example, or they will fail to acquire accurate information from the light that reflects off of objects. If one is to build a seeing machine (see "Building .. "), one must provide the machine with information about physical regularities (laws and assumptions), information that the machine can use to interpret incoming information from the surrounding world in an unambiguous manner (see "Intro to Vision"). However, because assumptions are not laws, they can sometimes produce perception which does not correspond to what is present in the world (an illusion).
Illusions
 For example, a basic assumption
that seems to be built into our visual system is that the objects that
we see are from a three-dimensional world. So, if we are presented with
a two-dimensional drawing, our visual system tends to interpret the
image as if it were caused by three-dimensional objects. Look at the
picture to the left. It appears that the three men in the picture are
roughly the same height, right? We make that judgment even though the
drawing of the man at the back of the picture is much smaller than the
drawing of the man at the front of the picture. The drawing was made
to conform to the physical laws of projective geometry (i.e.,
the size of the objects in the picture vary inversely with the distance
portrayed in the scene). The further away you want the object to appear,
the smaller the image must be. If we were to build a machine that could
correctly analyze three-dimensional scenes, it would need to be programmed
with the laws of projective geometry, taking into account the
fact that objects that are further away will project a smaller image.
For example, a basic assumption
that seems to be built into our visual system is that the objects that
we see are from a three-dimensional world. So, if we are presented with
a two-dimensional drawing, our visual system tends to interpret the
image as if it were caused by three-dimensional objects. Look at the
picture to the left. It appears that the three men in the picture are
roughly the same height, right? We make that judgment even though the
drawing of the man at the back of the picture is much smaller than the
drawing of the man at the front of the picture. The drawing was made
to conform to the physical laws of projective geometry (i.e.,
the size of the objects in the picture vary inversely with the distance
portrayed in the scene). The further away you want the object to appear,
the smaller the image must be. If we were to build a machine that could
correctly analyze three-dimensional scenes, it would need to be programmed
with the laws of projective geometry, taking into account the
fact that objects that are further away will project a smaller image.
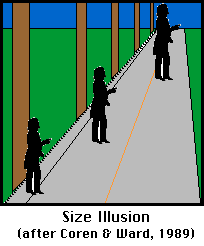 Next, let's consider a picture
that violates the laws of projective geometry (that is, the
size of the objects in the picture do not change with the portrayed
distance). When we look at that picture, the three men pictured do
not appear to be the same size. The man furthest down the road appears
to be much taller than the man in front. But, if you were to use a
ruler, you could confirm that the three figures are exactly the same
size. So this is an illusion. Things appear differently than they
really are. Of course it is good that we are susceptable to this illusion.
It results because our visual system has been adapted for use in a
three-dimensional (not a two-dimensional) world. This assumption --
that images projected onto our retina are reflected off of a three-dimensional
world (and thus subject to the laws of projective geometry) -- is
built into our visual system. If we are to build a machine that is
designed to recognize objects in a three-dimensional world, then it
too must have the same assumptions built into its visual system that
we have built into ours. If it does, then the machine will be subject
to the same illusion and it will determine that the men in the picture
above are not the same size. The machine will judge that the
further an object is perceived to be from the viewer, the smaller
the image it will project, because this is how light reflected off
of a three-dimensional world behaves.
Next, let's consider a picture
that violates the laws of projective geometry (that is, the
size of the objects in the picture do not change with the portrayed
distance). When we look at that picture, the three men pictured do
not appear to be the same size. The man furthest down the road appears
to be much taller than the man in front. But, if you were to use a
ruler, you could confirm that the three figures are exactly the same
size. So this is an illusion. Things appear differently than they
really are. Of course it is good that we are susceptable to this illusion.
It results because our visual system has been adapted for use in a
three-dimensional (not a two-dimensional) world. This assumption --
that images projected onto our retina are reflected off of a three-dimensional
world (and thus subject to the laws of projective geometry) -- is
built into our visual system. If we are to build a machine that is
designed to recognize objects in a three-dimensional world, then it
too must have the same assumptions built into its visual system that
we have built into ours. If it does, then the machine will be subject
to the same illusion and it will determine that the men in the picture
above are not the same size. The machine will judge that the
further an object is perceived to be from the viewer, the smaller
the image it will project, because this is how light reflected off
of a three-dimensional world behaves.
Illusions, then, are especially important in the study of vision, because they provide dramatic clues concerning the underlying assumptions that are built into our visual systems. Many "size" illusions can be explained in this way (Gregory, 1968) as arising from the assumptions that normally constrain processing to produce accurate (or veridical) perceptions of the real world.
The Müller-Lyer illusion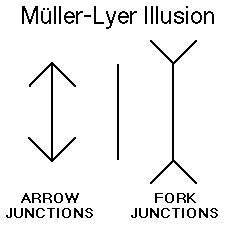 The Müller-Lyer illusion
is one of the oldest geometric illusions (Müller-Lyer, 1889/1981).
Lines with arrow junctions attached to the ends are perceived as shorter
and lines with attached fork junctions are perceived as longer, compared
to plain lines without junctions.
The Müller-Lyer illusion
is one of the oldest geometric illusions (Müller-Lyer, 1889/1981).
Lines with arrow junctions attached to the ends are perceived as shorter
and lines with attached fork junctions are perceived as longer, compared
to plain lines without junctions.
One hypothesis (Redding, 2000; Redding & Hawley, 1993) is that the size illusion is the result of our interpreting the line drawings as representations of three-dimensional corners. This is called the linear perspective hypothesis because it postulates that our visual system interprets the lines as a linear perspective drawing, which is a drawing that produces the impression of depth by projecting a three-dimensional scene onto a two-dimensional picture plane. When we view such a drawing our visual system attempts to solve the inverse problem by recovering the three-dimensional scene that would typically produce two-dimensional images of this kind (Kubovy, 1986).
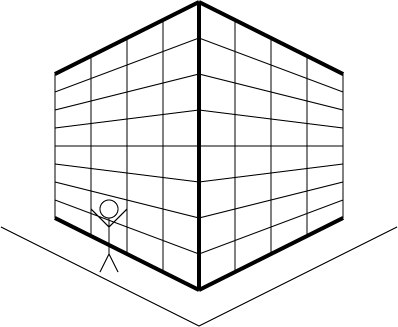
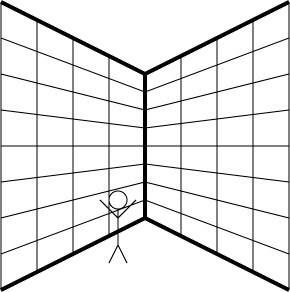
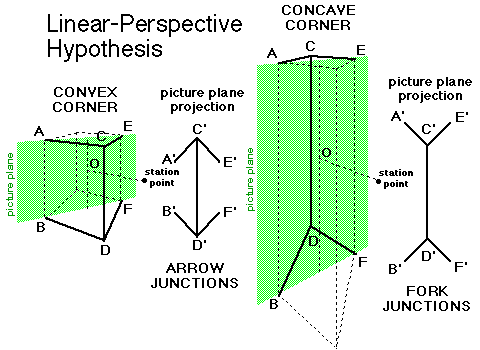
The Linear-Perspective Hypothesis The linear-perspective hypothesis assumes that the Müller-Lyer arrow and fork junction stimuli are interpreted by the visual system as linear perspective drawings depicting right-angled corners either projecting toward the viewer and in front of the picture plane (a convex corner) or projecting away from the viewer and behind the picture plane (a concave corner). We call a three-dimensional corner that is represented by a two-dimensional drawing, a "virtual" corner (because it isn't a real corner, it only looks like one).|
|
The image above shows the corner of a building projecting towards the viewer with the walls on either side receding away from the viewer. If the corner of the building is perceived to be projecting in front of the picture plane, then the line representing the corner will be perceived as being closer to the viewer and thus shorter than a simple straight line located in the picture plane (remember the law of projective geometry).
|
Conversely, the image on the left shows the corner of a building that projects to the back of the picture plane with the walls on either side coming toward the viewer. If the corner of the building is perceived to be projecting behind the picture plane, then the line representing the corner will be perceived as being further from the viewer and thus longer than a simple straight line located in the picture plane. |
| (click twice) | |
In other words, if the corner of the building (i.e., the virtual corner) is receding into the distance, then that tells the visual system that it is further away and thus that it is really taller than the image it projects. That's why it is judged to be longer than a single line without fork junctions. If, on the other hand, the corner of the building is projecting out towards the viewer, then that tells the visual system that the corner line is very close to the viewer and thus it is judged to be shorter than a single line without the arrow junctions. Of course, the size of the two-dimensional drawing (what is called "the picture plane size") also influences perception and the illusion is never as large as the difference in virtual corner sizes would predict.
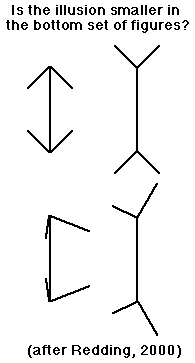 The linear perspective hypothesis makes sense, but is it
a good explanation of the illusion? One way of testing the hypothesis
is to derive from it predictions about how the illusion should change
in other conditions not yet observed.
The linear perspective hypothesis makes sense, but is it
a good explanation of the illusion? One way of testing the hypothesis
is to derive from it predictions about how the illusion should change
in other conditions not yet observed.
For example, if we mathematically rotate the virtual corners about the vertical axis in the picture plane, the corner size must also be changed to keep the same size in the drawing because the corners move closer to the picture plane. The rotated convex corner must be made larger and the rotated concave corner must be made smaller. This means that the illusions should decrease. Just this result has been found when drawings of rotated corners are presented to people for their judgment of size. The effect is small, but detectable (Redding, 2000).
Experimental tests of this kind can provide some evidence in support of a hypothesis (like the linear pespective hypothesis), but an hypothesis can never be "proved" because other explanations always remain possible (see "Methods for Studying Perception"). For example, there is a competing theory to explain the results of the experiments just described. The drawings of rotated corners have asymmetrical junctions (i.e, the junctions coming off the left side of the vertical line are not mirror images of the junctions coming off the right side of the line). It has been suggested that this asymmetry might itself be responsible for the decreased illusion. So how do you decide which theory to accept?
One of the best ways to look at data from experimental subjects who have responded to visual information that may be relevant to this question. Let's examine how the experiment was designed and why it might (or might not) provide support for the truth of the linear perspective hypothesis.