Return to MODULE PAGE
What is a Computer?
David Leech Anderson: Author
Why is it important to answer this question? Why do we need to try to decide what a computer is?
Computers play a formative role in the scientific study of the mind and brain. One important research method is to model a particular mental ability within a computer program. Many researchers in the field go further and claim that the mind is literally a computer program running on your brain (see section on Functionalism). But what is a computer? That is a matter of considerable controversy itself.
The upshot of all of this is that many debates about the nature of minds and cognition center on debates about how best to model cognition and whether the models in question are, or are not, computers. So the question, "What is a computer?" is not a trivial question about what definition one might find in the dictionary. Rather, it is a question that takes us right to the heart of some of the most exciting controversies in the field. So, let's jump right in and begin to explore some possible answers to this question.
Introduction
What is a computer? Well, one way to define a computer is that it is a machine that takes a rule or a recipe (what is usually called an "algorithm") and applies it to whatever it is instructed to apply it to. You do the same thing when you do addition.
When you "add up" the number of people in a room, you are performing the "add" function. You take a rule, let's call it the "add-1 rule," and you apply it to the human beings that occupy the room. You start with 0. You see one person and perform the "add-1 rule" on the 0 to get a new total of 1. You see another person and you perform the add-1 rule on your present total of 1, and and you get a new total of 2. And so on, until you've "added" the total number of people in the room.
Now let's say that there are many people in the room, that you are in a hurry and that you don't want to make any mistakes. So you decide to use a calculator to do the job and you ask a friend to help. Your friend starts calling out the names of each person in the room: "John, Sue, Mary, Bob, . . ." For each name called, you push the "+" and the "1" keys on the calculator.
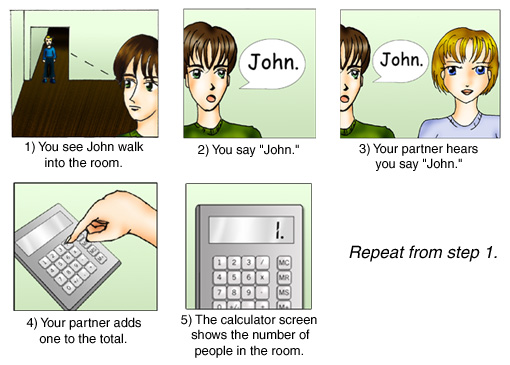
You have now turned the job of adding over to the calculator. Each time you push the "+" you are telling the machine to perform the "add" function; when you push the "1" you are instructing it to "add 1" to the running total. Another way of describing this is to say that after the "+" has been pushed (thereby turning the machine into an "adder") the calculator then takes two numbers as "input" and gives one number as "output". Let's say you've counted 14 people so far and your friend calls out a new name "Sidney". You then punch the "+" and the "1" keys. What the calculator does is to take two numbers (14,1) as input and to give one number (15) as output.
You might be surprised at how many things can be described as taking something as "input" and giving something else as "output." In the example above, we can describe the actions of you and your friend in this way. While the calculator may have relieved you of the responsibility of performing the "add" function, there are other "input-output" functions that you continue to perform.
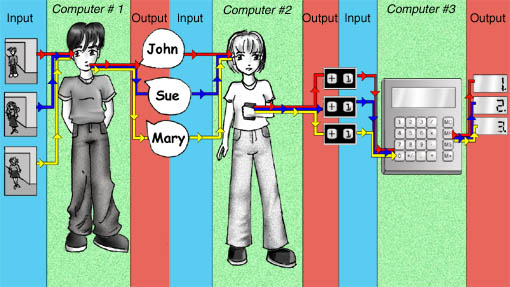
Your friend is performing the "name-calling function". Your friend takes as input the visual presence of a human being in the room and gives as output a spoken name (e.g. "Sue"). You, in turn, are performing what we might call the "change - name - to - number - and - push + function". You take as input what your friend gave as output: a name. For each name that you take as input, you give as output a "1" preceded by the "+" sign. So you take as input, "Sue," and give as output, "+,1".
We can think of you, your friend and the calculator as one single "person-counting system". We can then give a functional description of that system (just as we did with the heating system in the section on Functionalism). If we want a separate functional description for you, your friend and the calculator, then we put each of you inside an imaginary black box so that we see only the function that each of you perform but we do not see how you do it (or even that it is you doing it).
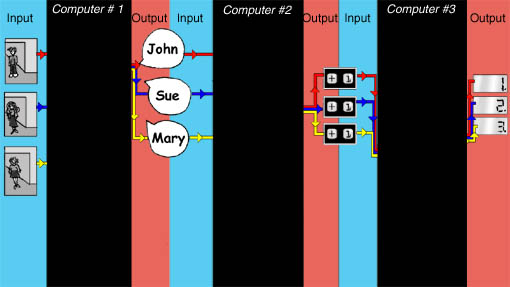
We have described you, your friend and the calculator as performing an input-output function. Does that mean that we can properly describe each of you as a computer? Well, that depends upon how you define "computer."
There are different ways of defining a computer depending upon what kind of function you think a computer must perform or implement to qualify as a "computer." Before we can understand the different kinds of computers that exist, we must briefly explore the different kinds of functions that a machine (or human) might implement.
What all functions have in common is that they take something as input and give something as output. To know that something is a function in this sense, we don't need to know anything about how it arrives at its output. All that matters is that there is a regularity in the way it determines the output. This is the broadest, most general concept of a function. In the long run, we are going to consider a variety of quite different types of functions. For the moment, however, we are going to focus our attention on the most familiar type of function -- those that always give exactly the same output for the same input. It is this type of function that lies at the heart of digital computers, the most familiar type of computer. (Later we will explore the fascinating case of "probabilistic" computers, which implement a broader type of function which does not always give the same output for the same input. Some people refuse to call these machines, "computers" and to call the rules that they implement, "functions". But more on these later.)
Our focus now is on what is, for most of us, the very paradigm of a computer: the digital computer. A digital computer implements functions that are precise, explicit and exceptionless. Now two people (or two machines) might be executing the same "function" in the broad sense (i.e., both always give the same output for the same input) but they might be doing it in different ways -- according to different rules.
Let's say that we know that something takes two numbers as input and gives as output a third number, which is the product of the first two numbers. We know, then, that this thing performs the multiplication function. But we don't yet know what specific rule or algorithm it follows to produce that output. One machine might use a different algorithm than does another -- and yet both equally qualify as performing the multiplication function, in this broad sense of 'function' that we are using.
Algorithms
We are familiar with machines that perform the operations of arithmetic (like addition and multiplication), what we would call, arithmetical functions. It is possible to write a computer program that performs arithmetical functions because these arithmetical functions (e.g., addition and multiplication) are computable functions. For a function to be computable, it must admit of an algorithm. An algorithm is a step-by-step mechanical process which, if followed faithfully, is guaranteed to produce the correct output (the "answer") for any input. The rules that a calculator follows when it performs arithmetic are all algorithms.
Consider multiplication. Any set of rules that takes two numbers as input and gives as output the product of those two numbers, will be a multiplication function. In this sense of function, we don't care how the rule produces the output, we only care what the output is for any given input. So, two different rules (two different algorithms) can both be multiplication functions. This means that there is more than one way to write a computer program for a calculator that can do multiplication. Here is one familiar set of rules -- one algorithm -- for performing multiplication (see Table 1):
Table 1: An algorithm for doing multiplication by multiple additions:
|
STEP 1 |
LIST each input item in a column, aligning each input to the right, then draw a line beneath the last item. |
4 |
|
STEP 2 |
ADD the units digits. Place the unit digit of the sum beneath the line in the unit's digit column. If the number is greater than 9, place the 10's digit of the sum above the first number in 10's digit column. If there is no such column, place the 10's digit of the sum beneath the line in the 10's digit position. STOP. |
4 |
|
STEP 3 |
ADD the 10's digits. Place the 10's digit of the sum beneath the line in the 10's digit column. If the number is greater than 99, place the 100's digit of the sum above the first number in 100's digit column. If there is such column, place the 100's digit of the sum beneath the line in the 100's digit position. STOP. |
4 |
This is one set of rules for doing multiplication. But there are others.
You could also write a computer program to perform multiplication using
the rules in Table 2.
Table 2: Another algorithm for doing multiplication that uses a "look-up" table.
|
STEP 1 |
LIST each input item in a column, aligning each input to the right, then draw a line beneath the last item. |
3 |
||||||||||||||||||||||||||||||||||||
|
STEP 2 |
Consult multiplication table:
|
|
||||||||||||||||||||||||||||||||||||
|
STEP 3 |
Locate the first number (3) in the horizontal column. Locate the second number (4) in the vertical column. Locate the number in the square that forms the intersection of the horizontal and vertical columns (12). Write that number below the line. STOP. |
3 |
This shows that two different computer programs, following different rules (or algorithms), can both be giving exactly the same output for a given input. They perform the same general multiplication function, even though they do it different ways.
In summary, then, digital computers are machines that perform (or implement) algorithms. But there are other machines that may deserve the title, "computer," even though they do not implement algorithms. We will call such computers "Non-classical" computers, and we turn to a discussion of these machines next.



