Return to MODULE PAGE
Introduction to the Scientific Method
Robert Stufflebeam: Author
Empirical claims
An epistemology is a theory of knowledge. Modern science is predicated on the epistemological view called empiricism. According to this view, we are not born knowing anything about "the world." Empiricists acknowledge that we are born knowing how to do certain things due to our instincts and reflexes (e.g., to cry, to eat, to perceive, etc.). But insofar as knowing that anything is true, empiricists believe that the mind is a "blank slate" -- or "tabla rasa" -- echoing the view championed by the empiricist philosopher John Locke in his An Essay Concerning Human Understanding(1690).
So, if we are not born with knowledge about the world, how is it acquired? In a word, experience -- from our observations and perceptions, as well as those of others. Knowledge gained through experience is called empirical knowledge. Science contributes to our empirical knowledge by providing the theoretical frameworks and research methods within which we are able to describe, to explain, and to predict the nature of "the world" successfully. And make no mistake about it. Science has been very successful.
Yet despite the deep understanding of the world that we have gained through science, there is an important feature of empirical knowledge that is worth noting at the outset. It is expressed as the claim in the following argument:

So, what should we conclude from this? That we do not know anything about the world? That science is unreliable? That we should not believe what science textbooks teach us? It may be comforting to hear that none of these things follow. But to see why this is so, you need to understand something about empirical claims -- assertions about how the world was, is, or will be. And the first thing to note is that every empirical claim is a contingent statement -- an assertion that is neither necessarily true nor necessarily false. So, for any contingent statement, it COULD be true, it COULD be false. And whether a contingent statement is true depends on (or is "contingent" upon) whether what it asserts accords with the way the "the world" is. To put it baldly, if what a contingent statement asserts corresponds to "the world" in terms of either meaning (for words) or reference (for objects), then the statement is true. If this correspondence is not present, then the statement is false.
While this accounts for whether a contingent statement (or empirical claim) is true, it does not account for how we know it. Since our knowledge about the world (empirical knowledge) depends on our ability to tell whether a contingent statement is true, a great deal hinges upon the answer to this question: How do we know whether an empirical claim is true or false? Unsurprisingly, experience. Experience provides us with the evidence (justification) for believing that certain statements about the world are true while others are false. For example, consider the following empirical claim:
If someone’s brain leaves his body, he will die.
Is this claim true? Yes, we believe so. How do we know? Well, for starters, there has not been a single documented case in human history where an individual lost her brain and continued to live. And since experience has also taught us that brains regulate the respiratory and other bodily systems that are necessary for life, the evidence for the truth of this claim is overwhelming.
However, does all our "overwhelming" evidence guarantee that this claim will remain true in the future? No. After all, in much the same way that we can now replace a "real" heart with an artificial one, is it not possible that we could one day replace a "real" brain with an artificial one? The point is not whether such a procedure is probable, but whether it is possible. And it is. Hence, the above claim is neither necessarily true nor guaranteed to be true. Given what we know about human history and the present state of brain transplant technology, the above claim is true. But it could one day turn out to be false. Here is the rub: The same can be said for EVERY empirical claim. The reason for this is that no accumulation of empirical evidence (experience) will EVER guarantee that events in the future will occur as they have in the past. Consequently, not one empirical claim (or "fact" about anything in the world) is guaranteed to be true. This lack of a guarantee is called the problem of induction. And with respect to knowledge about the future based on past experience as evidence, it is insurmountable.
But this problem is not limited to empirical claims about the future alone. Rather, it also applies to empirical claims about both the present and the past. For instance, the best empirical evidence currently available leads us to believe that the following empirical claim is true:
Neil Armstrong was the first human to walk on the moon.
While the evidence for the truth of this claim is overwhelming, even "overwhelming" evidence can lead us to believe that a claim is true when it is in fact false. Such was the case with this claim:
Earth is the center of the universe.
Although the best evidence for centuries led people to believe otherwise, they were mistaken nevertheless. And as there are many fields of science that are littered with bodies of evidence that misled people to believe claims that were in fact false, there is every reason to believe that some of what we now believe to be true will be proven false as well. The above claim about Neil Armstrong is a candidate for this. Granted. It would take a great deal of evidence to convince us that this belief is false. Nevertheless, as it is possible that NASA perpetrated an elaborate hoax, it is possible to refute the "fact" that Neil Armstrong was the first human to walk on the moon. Indeed! There is not a single empirical claim that is immune from being proven false. Not one! So, even though it is very, very improbable that certain empirical claims will ever be proven false, it is possible that they could be proven false. And in principle, this is possible for EVERY empirical claim.
Thus, in order to justify our claims about the way "the world" was, is, or will be, we must rely upon empirical evidence. But since our empirical evidence is no more guaranteed to be true than the claims our evidence is offered to show, we are left with the inescapable conclusion that our knowledge about the world will never be perfect, certain, and unrevisible. Empirical knowledge just does not work that way. As such, here is the fundamental message to take home from this discussion: There are limits to what scientists can discover, understand, explain, and predict based on experience and observation as evidence. Here is another: It is NOT a weakness of science that no empirical claim is immune from possible refutation. After all, the reason that so many empirical claims (and theories) deserve to be believed is that they have (thus far) survived the scrutiny of researchers who consistently try to refute them through the scientific method. Let us turn our attention to how this occurs.
How do scientists reason?
It is not really the case that scientists reason differently than nonscientists. Reasoning is reasoning. Still, our focus is on scientific reasoning, specifically, on how empirical evidence bears upon the truth of scientific hypotheses. Toward this end, you need to understand a bit more about the nature of arguments and the role they play in the scientific method.
Arguments
As noted in the previous section, every empirical claim is either true or false (but not both). And making an empirical claim is easy. After all, doing so requires merely asserting something about the way the world was, is, or will be. Here are two examples:
Earth is flat.
It is false that Earth is flat.
Can both of these empirical claims be true? No. As they are contradictory, exactly one is true and exactly one of false. But which is which? Most of us believe that the second statement is the true one. Not everyone agrees, particularly members of the Flat Earth Society. Now is not the time to evaluate the reasonableness of the evidence that "justifies" their belief, for the point is this: There will always be an audience for whom a claim is obvious. Again, making claims is easy, especially in the presence of an audience who is predisposed to accept your claim is true. The hard part about making claims is convincing an audience who sees the world differently. There are innumerable occasions in science when a researcher must try to show, to persuade, to convince, or to prove to an audience that a particular claim is true. To succeed, the researcher must do more than merely assert her claim. Rather, she must argue for it.
But what are arguments? Well, "good" ones are the medium through which we plan, explain, persuade, convince, and prove things successfully through language. And not only does every argument in the universe consist of a set of statements, every argument, no matter how complicated, consists of only two functional parts. One is the claim, the statement asserted to be true. The other is the evidence, the statement(s) purporting to show that the claim is true. It really is that simple.
But while arguments are used for many purposes in science -- to explain, to persuade, to convince, to predict, to demonstrate, and to prove things through language -- it is not the case that the hallmark of science is offering arguments. Instead, the hallmark of science is conducting tests. Scientific tests are a kind of argument that requires performing an experiment, investigation, or research for the sake of resolving an empirical question. As you might expect, what makes a question an empirical one is the need for experience and observation to answer it. Consider this one:
How many planets are there in our solar system?
Is it possible to answer questions of this sort correctly without relying upon evidence from experience and observation? No (even "guessing" qualifies as experience). Yet neither is it possible to do so reliably without looking in the right place. Suppose that you were a researcher attempting to resolve how bats perceive the world through echolocation (a kind of "sonar"). Would you stand any chance of success by observing weather patterns in Antarctica, writing a pattern recognition computer program, or investigating the effects of vodka upon feline perceptual abilities? Of course not. Successfully resolving an empirical question requires conducting not just any scientific test, but one that results in evidence that is relevant to the question. Not all experiences and observations are relevant to all questions. Neither are all research methods and techniques.
So, when attempting to settle an empirical question, how does a researcher decide where to observe, which experiences to record, and what evidence is relevant? The answer has two parts.
First, since it is impossible to conduct a scientific test without the use of a particular experimental technique or method, the method chosen by a researcher will determine which experiences to observe and record. For instance, suppose that you wanted to know whether you have a fever. Because you assume that your old-fashioned thermometer is in good working order, you take your temperature. What do you look for? The mercury level against the temperature scale? Of course. While you may also observe the manufacturer of the thermometer, the color of its numbers, and a host other things about the instrument, your having chosen an old-fashioned thermometer makes the observations that are relevant to this test different from the observations that are relevant to a test using an electronic thermometer. Obviously.
Second, even when a researcher does not do so consciously, she decides where to observe, which experiences to record, and what evidence is relevant by making inferences. Every inference is the conclusion of a "mini" argument. Therein lies the relation between arguments and tests: It is through arguments that researchers identify the empirical consequences of their assumptions. Because scientific tests are impossible without the evidence-claim relation present in every argument, arguments are an inseparable part of the scientific method.
The scientific method
Although empirical questions engender scientific tests, strictly speaking, scientific tests are not tests of empirical questions. After all, questions are neither true nor false. Empirical statements, yes, they have truth-values, but empirical questions do not. So, because scientific tests are conducted in order to augment our knowledge about the world, and knowledge about the world is expressed via true contingent statements, a scientific test is a test of a contingent statement. What that statement is will be an answer to an empirical question. Regardless of whether that answer is tentative, "unproven," or an established "fact," any statement subject to an empirical test is an hypothesis. Hypothesis testing lies at the heart of the scientific method. What follows is an outline of the procedure. And to make things more concrete, suppose that you are a medical doctor. A patient arrives who you have never before seen and the patient claims to be pregnant.
STEP 1:CHOOSE AN EMPIRICAL QUESTION
Because scientific tests bear upon resolving empirical questions, but not necessarily philosophical ones, conducting scientific research requires dealing with a question that can be settled by experience and observation.
For our test, the empirical question (Q) is this: Is the patient pregnant?
STEP 2:CHOOSE A HYPOTHESIS
The key to a scientific test is the hypothesis (H). Usually, the hypothesis is the statement asserting what a researcher assumes is the correct answer to whatever empirical question is motivating the research. But since scientists sometimes test competing hypotheses or those of their colleagues, from a logical point of view, it makes no difference whether a scientist "really" believes in the truth of the hypothesis being tested. The only thing that matters is that something is assumed to account for, to explain, or to otherwise be the correct answer to the question, even if only for the sake of argument.
For our test,
H = The patient is pregnant.
And H is the first empirical evidence statement within the argument of the test:
1. Let's assume that H.
STEP 3: CHOOSE AN EXPERIMENTAL TECHNIQUE/METHOD
No empirical question can be settled without reports of experience. That is, the test must produce something that we can detect with our five senses (something we can see, hear, touch, smell, or taste). Thus, testing an hypothesis requires choosing a method that produces observable data. The data may be directly observable by the researcher, as is the case when a physician examines a patient and relies solely upon what she sees, hears, and feels without the aid of any instruments. Indirectly observable data is obtained through the use of an instrument. For instance, you can indirectly observe (a) someone's temperature via a thermometer, (b) a cell's membrane via a microscope, (c) a distant galaxy via a telescope, etc.
So, what technique/method should we choose for our test? Let's opt for a blood test -- a test measuring the amount of HCG (human chorionic gonadotropin) in the blood. HCG is the hormone made within a woman's body after an egg is fertilized and starts to grow into an embryo. Incidentally, HCG is also detected in urine pregnancy tests.
STEP 4: IDENTIFY THE ASSUMPTIONS
While the hypothesis is an assumption (A), the hypothesis will NEVER be the only assumption made when the scientific method is used. The reason for this is that EVERY evidence statement within an argument is an assumption -- a statement whose truth is being presupposed but not proven. After all, you can't do everything at the same time. You bear the burden of showing that your claim is true when you argue, not for showing that your evidence is true. Granted, if someone challenges your evidence, you may then be required to give another argument to support your evidence. But that would be a different argument. You can only do one thing at a time. Thus, assumptions are a necessary part of every argument.
The additional assumptions may be either explicit or implicit. The explicit assumptions will be the additional stated evidence statements within the argument. One most common evidence statements of this sort are scientific laws -- statements to the effect that in such-and-such part of the universe, whenever conditions of a particular kind occur, F, then, all things being equal, conditions of another kind, G, will also occur. Scientific theories are another kind of explicit assumption commonly found among the stated evidence statements in arguments of this sort. A scientific theory is a testable set of general principles that explain a range of observed phenomena.
Implicit assumptions, while not stated evidence statements, are evidence statements nevertheless. And EVERY statement (and question) carries implicit assumptions. For example, consider our hypothesis. If you as the physician assume that the patient is pregnant, then you are implicitly assuming that each of the following statements is also true:
- The patient exists.
- The patient is a female.
- Some patients can be pregnant.
- Only females can be pregnant.
- It is possible for the patient to be pregnant.
Moreover, every research method carries implicit assumptions too. Thus, to the list of implicit assumptions just identified, we can add the following:
- Blood exists and so do sex hormones.
- It is possible to extract a patient's blood.
- It is possible to test blood for hormone levels.
- HCG is a hormone.
- HCG is made when and only when a woman is pregnant.
- The presence of HCG is a reliable indicator of pregnancy.
Now, are any of these implicit assumptions unreasonable? No. Consequently, do not consider assumptions to be "bad" evidence. By all means, consider dubious assumptions to be "bad," but 'dubious assumption' and 'assumption' do not mean the same thing.
Of course, every theory carries implicit assumptions as well, but I suspect you get the idea.
Although I want you to understand the logical structure of the scientific method, it makes no sense to complicate things unnecessarily. Hence, rather than identify each explicit assumption as a separate evidence statement, let's represent the set of auxillary assumption as '{A}'. Here is the argument so far:
1. Let's assume that H is true.
2. Let's assume that {A} is true.And if the hypothesis and our set of other assumptions is each true, we may infer that the following conjunction must be true too:
3. H and {A}.
STEP 5: INFER THE LOGICAL CONSEQUENCES OF THE ASSUMPTIONS
Whether the scientist does so consciously or not, it is at this point when she asks herself the following question:
If my hypothesis and other assumptions are true, then what event must I observe in the world?
After all, if the assumptions are true, then certain observable events must occur under the specific circumstances determined by the choice of method. The logical consequences of the assumptions are those observable events (O).
Note that the researcher is not interested in what she may observe, but what she must observe. For instance, if our hypothesis AND our other assumptions are true, does it follow that the patient must have a distended belly? No. The patient may be only one month pregnant or too large for her pregnancy to be seen. Does it follow that the patient will have experienced morning sickness or cravings? No. It is possible to be pregnant and experience neither of those common symptoms.
So, if the truth of our hypothesis AND our auxiliary assumptions does not entail either of these observations, what do they entail? What must we observe? While there are several obvious candidates, the observable event (O) most relevant for our purposes is this: HCG should be detected in the patient's blood.
Here is the logical structure of the test so far:
1. Let's assume that H.
2. Let's assume that {A}.
3. H and {A}.
4. If H and {A}, then O.
STEP 5: PERFORM THE TEST AND RECORD THE DATA
Having set up the test (in the form of an argument) to identify what should be observed if the hypothesis and other assumptions are true, it is at this point when the test is completed and the observations ("data") are recorded. There are two possibilities. Either what was observed was what should have been observed, or, what should have been observed was not observed. Either way, having recorded what was observed, the evidence is now complete. The final step in a scientific test is to evaluate the hypothesis in relation to that evidence.
But an empirical argument consists not just of evidence. An empirical claim is supposed to follow from that evidence. Because a great deal of emphasis has been placed on how scientists choose their evidence (assumptions), you may be wondering why no attention has been directed at the claim itself. The reason for this is that a scientist uses the scientific method to determine whether his hypothesis is true. While this may sound obvious, there is a significant difference between making a claim and then assuming certain evidence in order to show that the claim is true, on the one hand, and assuming the truth of an hypothesis (and other assumptions) in order to see what follows. The former characterizes the use of virtually all argumentative reasoning outside the context of a scientific test. The latter characterizes one of the defining features of being a "good" scientist; namely, being willing to abandon an hypothesis if the evidence does not support it. Contrary to popular belief, it is not the purpose of the scientific method "to prove" an hypothesis, but to make certain assumptions and observations (evidence) explicit in order to maximize the chances of evaluating an hypothesis accurately.
STEP 6: EVALUATE THE HYPOTHESIS
Empirically speaking, whether what should have been observed was observed is the crucial piece of evidence that bears upon whether the hypothesis is true. As noted above, there are two possibilities. One is positive (because what was observed was what should have been observed). The other is negative (because what should have been observed was not observed). Logically speaking, things are not quite so simple. Let's deal with the easiest case first.
Negative case
It is often said that negative data (not seeing what should have been observed) falsifies the hypothesis. But that is not necessarily true. What does logically follow from negative data is H and {A} are not both true. In other words, either the hypothesis is false or at least one member of the set of auxiliary assumptions is false. A test with negative data (evidence statement 5) results in the following argument:

As this argument is valid, the claim follows necessarily from the evidence. And because it is impossible for a valid argument to have true evidence and a false claim, if evidence statements 1-5 are true, then necessarily the claim must be true too. Therein lies the value of validity: If an argument is valid AND all its evidence is true, then the claim MUST be true too (not on its own necessarily, but only in relation to the evidence).
So, if our test results were negative, it follows that either the patient is not pregnant or one of our other assumptions is false ("dubious"). Which is more reasonable to believe? As is the case with most empirical research, it is usually the hypothesis that is less well accepted than the methodological, theoretical, and other auxillary assumptions. Thus, a negative test usually results in a hypothesis being abandoned or revised. And since the empirical question motivating the research has not been resolved, negative tests lead to further research. For that reason, negative data is not a "bad" thing. Besides, it is the scientist's job to discover truths about the world, not to defend a pet hypothesis against unfavorable evidence. Indeed! Where it is not possible to test an hypothesis (or theory), it is not possible to falsify it. Hypotheses (or theories) that are "true" no matter what can be observed in the world are not scientific (e.g., astrology). Rather, such hypotheses (or theories) are pseudoscientific. Pseudoscience is always "bad" science.
Positive case
It is often said that positive data (seeing what should have been observed) verifies the hypothesis, showing that it is true. Hence, a test with positive data (evidence statement 5) results in this argument:
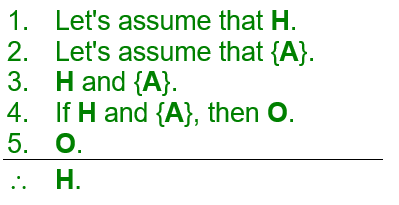
But take a closer look at this argument. Does anything strike you as suspicious? Hopefully so, namely, that the first evidence statement and the claim are one and the same statement. Do you see this? It may help to note that while the expression 'let's assume that' make the first and last statements different sentences, what each of those sentences asserts is one and the same statement -- H. Whenever something like this occurs, the argument is said to be circular (or beg the question). Because it is logically impermissible to presuppose the truth of your claim among your evidence when you are trying to show that your claim is true, every circular argument is a bad argument. But since it is impossible for the evidence to be true and for the claim to be false, owing to its circularity, every circular argument is a valid argument. However, we know this before we even perform the test. We can simply ignore statements 4 and 5 because the claim follows directly from statement 1 (as well as statement 3). And as the observed "data" is logically irrelevant to the truth of the claim, it makes no sense to say that the observation verifies the hypothesis.
If there is a good argument to be constructed here, how are we to do it? First we have to recognize that there are different types of arguments. Some arguments are so structured that the truth of the premises (the assumptions) guarantees the truth of the claim being defended. In such deductive arguments, the claim necessarily follows from the assumptions. But there are many good arguments that do not have this characteristic. In fact, most of the arguments given to support scientific claims -- even the really good arguments -- do not have this property. This is because most scientists offer arguments in which the claim being considered is supported by evidence that makes the claim probable (often highly probable) but that does not logically guarantee the claim. We call arguments of this kind inductive arguments. Because science is concerned with learning contingent facts about the world that can never be guaranteed to be true, the strongest support that can ever be offered for these claims is the inductive support that comes from inductive arguments. If we eliminate evidence statements 1-3, the resulting argument no longer begs the question. Moreover, it captures the rationale for believing that the positive data (evidence statement 2) verifies the hypothesis:

For example, consider the empirical claim that the sun will rise tomorrow. Notwithstanding 5 billion or so years of evidence for the truth of this claim, due to the problem of induction, there is no guarantee that the sun will rise tomorrow. It is possible that aliens from another galaxy will blow the sun out of the sky tomorrow. If they do, the sun won't rise. But that isn't likely. Does the lack of a guarantee mean that the claim is not very very likely to be true? No. And clearly it is very very likely to be true. Therein lies the value of induction.
Hence, inductively, it does make sense to say that the "observed" data verifies the hypothesis. While it does not follow that the hypothesis is true, it does follow that the evidence justifies our belief that it may be true. In our test, would a positive blood test guarantee that the patient is pregnant? No. The patient may have a hormonal imbalance, the test results may have been switched with another patient, etc. Nevertheless, unless there are reasons for believing that one of these possibilities occurred, we would be justified to believe that our hypothesis is true. All things being equal, the same holds for other "verified" hypothesis. But since no empirical claim is necessarily true, remember, no verified hypothesis, "fact," or any other statement about the world is immune from possible refutation.
Here ends your introduction to the scientific method and how scientific tests contribute to our knowledge about "the world." The principle benefit of having explored the general nature of scientific research is that you should be sensitive not just to the limits of scientific research, but to the role of assumptions (theoretical, methodological, etc.) within both arguments and scientific tests.
FUNDING:
This module was supported by National Science Foundation Grants #9981217 and #0127561.



