Return to MODULE PAGE
Connectionism (page 1)
Robert Stufflebeam: Author, Artist & Animator
What is connectionism?
Connectionism is the name for the computer modeling approach to information processing based on the design or architecture of the brain. Not the architecture of the whole brain mind you. Rather, because neurons are the basic information processing structures in the brain, and every sort of information the brain processes occurs in networks of interconnected neurons (neural networks), connectionist computer models are based on how computation occurs in neural networks.
There are many kinds of connectionist computer models -- connectionist networks. Some are designed for tasks that have nothing to do with modeling biological neurons. Other models are offered as a way to understand how "real" neural networks work. These models are called artificial neural networks. For now, we do not need to worry about whether a particular connectionst model is merely a connectionst network or if it is an artificial neural network. The reason for this is that all connectionst models consist of four parts -- units, activations, connections, and connection weights. Each of these parts corresponds to a particular structure or process in biological neural networks. To see this, let's first take a look at the anatomy of a connectionst model. Then let's take a look at how such models work.
Anatomy of a connectionst model
Units are to a connectionist model what neurons are to a biological neural network -- the basic information processing structures. While it is possible to build a connectionist model with tangible units -- objects that can be touched as well as seen -- most connectionist models are computer simulations run on digital computers. Units in such models are virtual objects, as are the pieces in a computer chess game. And just as you need symbols for the pieces in order to follow a virtual chess game, the "pieces" in a connectionist computer model need to be represented in some fashion too. Units are usually represented by circles. Here is a unit.
Because no unit by itself constitutes a network, connectionist models typically are composed of many units (or at least several of them). Here are 11 units:
But no mere cluster of units constitutes a network either. And you will never see a connectionist model "organized" in this chaotic fashion. After all, not just any grouping of units corresponds to the architecture of biological neural networks. "Real" neural networks are organized in layers of neurons. For this reason, connectionist models are organized in layers of units, not random clusters. In most connectionst models, units are organized in 3 layers. (Incidentally, the cerebral cortex, the convoluted outer part of the brain, is organized into 6 layers.) So, reorganized in 3 layers of units, the following organization of units mirrors the structural organization of many connectionist models.
But what you see here still isn't a network. Something is missing. Can you tell what that "something" is? For a hint, take a look at the pair of images below. The one on the left does not capture a computer network. The one on the right does. What makes the image on the left an image of 6 computers, but the one on the right an image of a computer network?
The connections! The computers on the right are connected to one another. Because no group of objects qualifies as a network unless each member is connected to other members, it is the existence of connections between the 6 computers on the right that makes them a computer network.
Of course, not just any physically connected group of computers qualifies as a computer network. For example, the connections in the above computer network are represented with lines. What kinds of "things" do the lines represent such that the combination of computers plus the connections results in a computer network? Any of the following kinds of connections would be acceptable: ethernet cables, telephone wires, or wireless transmissions. But "connections" made from the following materials would not:pipes, ropes, . . ., or spaghetti. Can we "connect" a group of computers together with such things? Sure. But a network is NOT simply a interconnected group of objects. Rather, it's an interconnected group of objects that exchange information with one another! Although it is true that a physical connection in a computer network can be implemented in a variety of ways (e.g., through a cable, a wire, or wireless transmission), not just any physical connection will permit information to flow from one computer to another. Thus, generally speaking, network connections (or simply connections) are conduits through which information flows between members of a network. In the absence of such connections, no group of objects qualifies as a network.
There are two kinds of network connections. An input connection is a conduit through which a member of a network receives information (INPUT). An output connection is a conduit through which a member of a network sends information (OUTPUT). Although it is possible for a network connection to be both an input connection and an output connection (depending on the direction in which the information is flowing), no computer qualifies as a member of a network if it can neither receive information (INPUT) from other computers nor send information (OUTPUT) to other computers. For instance, consider the lesson ("information") you are now reading. You cannot access it from just any computer. Instead, you can access this lesson only from a computer connected to the Internet -- the largest of all computer networks. And just as your computer cannot receive information via the Internet unless it is connected to the Internet, a computer not connected to the Internet cannot send information via the Internet either. A computer that can neither receive information via the Internet nor send information via the Internet is not a member of the Internet.
Is the function of connections in a neural network the same as the function of connections in a computer network? You bet! In fact, the function of a network connection is the same regardless of whether the network is composed of computers, neurons, people, units, or anything else. Consequently, the function of connections in neural networks is to be conduits through which neurons receive INPUT from other neurons and send OUTPUT to other neurons. Neurons are to neural networks what computers are to computer networks. But what functions as connections in a neural network? To answer this question, take a look at the following picture. It consists of three neurons -- A, B, and C. As the picture depicts, A is connected to B, which is connected to C. Information flows from left to right. Hence, the OUTPUT of A is the INPUT to B, and the OUTPUT of B is the INPUT to C. Since the flow of information in a network occurs through its connections, where are the connections in this "mini" neural network?
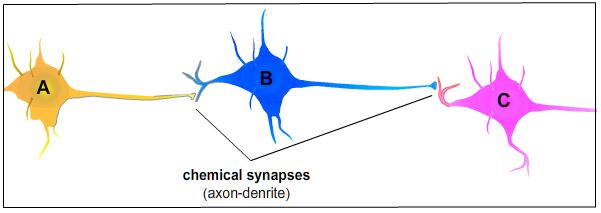
The synapses! Synapses are to neural networks what an ethernet cable or telephone wire is to a computer network -- conduits through which information flows from one member of the network to the next. Without synapses (connections) from other neurons, it would be impossible for a neuron to receive INPUT from other neurons. And without synapses (connections) to other neurons, it would be impossible for a neuron to send OUTPUT to other neurons. Given the crucial role connections play in a network of neurons, synapses (connections) in a biological neural network matter as much as the neurons themselves. And because connectionist models are based on how computation occurs in biological neural networks, connections play an essential role in connectionist models -- hence the name "connectionism."
As you already know that units in a connectionist model are analogous to neurons, you should not be surprised to hear that connections are analogous synapses. And just as units need to be represented in some fashion, so too do connections. Connections in a connectionist model are represented with lines. As such, to avoid confusion, it is worth emphasizing that connections within a biological neural network are synapses, not dendrites and axons. Dendrites and axons are parts of neurons. Synapses are not. In fact, synapses are "gaps" between neurons -- the fluid-filled space through which chemical messengers (neurotransmitters) leave one neurons and enter another. Consequently, these "gaps" are connections between neurons, not dendrites and axons. For instance, take another look at neuron B above. B receives INPUT from A through a synapse at its dendrite. B's outgoing information "flows" down its axon to an axon terminal, then through a synapse to a dendrite of C. Although it is reasonable to think of dendrites and axons as conduits through which information flows within a neuron, a neuron's dendrites and axon are part of its structure. Synapses are not. Synapses are where information "flows" from one neuron to another. Hence, connections within a neural network are synapses. (See Introduction to Neurons, Action Potentials, Synapses, and Neurotransmission for a more detailed study of how neurons work.)
Here is a useful computer analogy: The computer from which you are reading this lesson is a member of a computer network. But the network connection through which your computer receives information and sends information isn't the only INPUT and OUTPUT connections your computer has. After all, your computer is itself a network consisting of INPUT devices (e.g., keyboard, mouse, etc.), OUTPUT devices (monitor, printer, etc.), and connections from these devices to your computer's CPU -- the place where information processing occurs. Consequently, think of the cell body of a neuron as the CPU of your computer system. Think of a neuron's dendrites and axon as the cables connecting your CPU to its INPUT and OUTPUT devices. On this analogy, a synapse is the cable or wire through which you exchange information with other computers on the Internet. Since a unit in a connectionist model is analogous to a neuron, consider a unit to be your entire computer system minus the network connection.
Because units in a connectionist model are represented with circles, each circle is analogous to an entire neuron -- its dendrites, cell body, axon, and axon terminals. Connections in a connectionist model are represented with lines. Notwithstanding how lines might resemble dendrites or axons, each line is analogous to a synapse. Arrows in a connectionist model indicate the flow of information from one unit to the next. And since any one neuron in the brain can be connected to thousands of other neurons, a unit in a connectionist model typically will be connected to several units. Some of those connections will be INPUT connections from units at a lower level; others will be OUTPUT connections to units at a higher level. To illustrate, take a look at the blue unit in layer 2 below. As is common in connectionist models, the blue unit is connected to each of the units above it and below it.
From which units does the blue unit receive its INPUT? To which units does it send its OUTPUT? Well, its INPUT is received via connections from each of the units in layer 1. Given the flow of information from bottom to top, the OUTPUT of the units in layer 1 becomes the INPUT to the blue unit. The blue unit is connected to each of the units in layer 3. Hence, the OUTPUT of the blue unit becomes the INPUT to each of the units in layer 3.
When each unit in a connectionist model is connected to each of the units in the layer above it, the result is a network of units with many connections between them. This is illustrated in the following figure. It captures the architecture of a standard, 3-layered feedforward network (a network of 3 layers of units where information flows "forward" from the network's INPUT units, through its "hidden" units, to its OUTPUT units).
Just as it is important for you to understand the architecture of connectionist models, it is important for you to understand how such models work. To to this, you must understand the nature of unit activations and connection weights -- the other two "parts" of connectionist models besides units and connections. Because unit activations and connection weights are essential "parts" of how information processing occurs within a unit, let us turn out attention to how units receive INPUT and produce OUTPUT.



