Return to MODULE PAGE
The Science of Vision: An Introduction
David Leech Anderson: Author
Rob Stufflebeam: Animations
For those of us blessed with sight, it is difficult not to take it for granted. Every day of our lives and for virtually every waking minute we depend upon our vision. But how does our visual system work? For that matter, how is vision even possible?
We live in a three-dimensional world of great complexity and immense proportion. Light reflects off of that world and strikes the retina, a small patch of tissue at the back of the eyeball. We see a rich 3-dimensional world of remarkable subtlety, and it all comes from that tiny patch of light-sensitive cells. How does that meager input produce such a torrential output of information about the world?
How in the world is vision possible?
It may seem, at first, a simple matter. One may be tempted to think this way: "Well, a camera can do it, why should it be so hard for the human eye to do it." But a camera doesn't do it. The picture a camera produces is a two-dimensional patch of shades and colors. It "feels" to us as if a two-dimensional photograph reproduces a three dimensional world -- but it doesn't. We are the ones who see flat pictures as pictures of a three-dimensional world. The same visual system that interprets the world around us, also interprets the photograph to make it "appear" as a three-dimensional world.
Let's see how it might work. The first step in the process is not so mysterious. We know from the study of optics how light behaves when it passes through a lens. The eye has a lens, much like the lens of a camera, that takes all of the light that comes from the environment and focuses it onto the retina of the eye, which lies a short distance behind the lens.
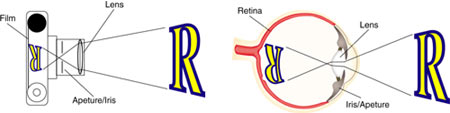
Notice that the image reflected on the film of the camera and on the retina is upside down. So the first bit of visual processing that must be done by the visual system is to turn the image "right-side up" -- which the brain does quite handily.
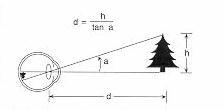
Another step in the process is to perceive the size of the objects accurately. This is a more difficult task than it might first appear. We know from optics that the size of the image projected on the retina is determined by the size of the object and the distance of the object from the perceiver. Two objects of the same height will not project the same size image on the retina if one of them is further away than the other.

The more distant object projects a smaller size image on the retina. Let's assume that there are two objects of equal size but at different distances from the viewer (picture A). It will then be the case that
- The images projected on the retina will be two dimensional and upside down, and
- The closer object will project a larger image than the further object (picture B)
This relationship between the size and distance of the object and the size of the image projected on the retina, can be captured in a precise formula:
While the more distant object projects a smaller image on the retina, it does not appear to be smaller than the closer object. We perceive both objects as being roughly the same size. And we don't see them as being flattened into a two-dimensional space, but as occupying three-dimensional space, with one object located far back into the depth of 3D space.
But how do we accomplish this feat? The task is a challenging one. First, light reflects off of objects in the world. The light is then focused by the eye's lens and it strikes the retina, projecting an image. The objects in the world that are projecting the image we refer to as the distal stimulus. The light striking the retina and creating the 2D image is called the proximal stimulus.
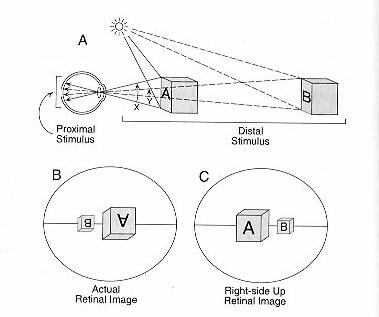
The job of our visual system is to take the information that it receives from the world (the proximal stimulus), which in the case above is something like the two-dimensional, upside-down image in B and with this limited input it must produce in us an experience of the rich three dimensional world (the distal stimulus).
How can the visual system tell whether the image reflected on the retina is a small object nearby, or a large object far away? And how can it tell if it is a short object standing straight up and down or a long object laying out toward the horizon? The problem arises in this way.
Consider a case where a line is projected on the retina, as in the image above. What is the size and orientation of the object that causes the line to be projected? First, it could either be a skinny rod or a rectangle turned on its side. But even if we were somehow able to rule out the rectangle possibility, there are still many different lengths and orientations of "skinny rod-shaped objects" in a three-dimensional world that might be projecting a line of that very length on our retinas. Consider the five different objects below that might cause such a line to be projected onto the retina.
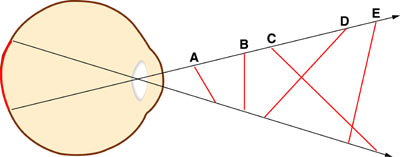
Assume that the first line, (a), is a small stick held at an angle a few inches from the eye; (b) is a chopstick standing straight up-and-down a foot away; (c) is a round curtain rod and (d) a piece of wood dowling; and finally (e) is a polevault laying out into 3D space some distance from the viewer. If all of these objects were positioned in just the right way and at the right distance from the viewer -- each 3D object could project a line of precisely the same length and diameter onto the retina. In fact, there are not just five or six actual object sizes that could produce the two-dimensional projection, there are an infinite number of such objects.
How does the brain figure out which is the right one? A problem similar to the one that arises for lines, also arises for surfaces. A two-dimensional image (the image on the retina) must inform us about a three-dimensional world. But there are an infinite number of quite different three-dimensional world situations that would project the same basic two-dimensional image on the retina. To demonstrate the problem with surfaces, consider the image below. First, count the number of objects that you see.

If you said that there were four objects, then you probably see the image the way most people do. Push the green "play" button on the image below and see if this is the way that you were interpreting it.
A proper description of the picture, as we are interpreting it here, is to say that we see the circle as "occluded" by the triangle, the square "occluded" by the triangle, and so on. For one object to be occluded by another is for it to be partially obscured or hidden behind it. But why do we "see" the image in that way? After all, there is nothing in the image itself that points to a three-dimensional space with enough depth to allow four objects to lie one in front of the other. One might think that the more reasonable interpretation, given the information provided by the image, would be to interpret it as six different objects, not four. [Push "play" button.]
On this interpretation, the shapes are sitting side by side all occupying the same two-dimensional plane --like tiles on a floor.
We now have two competing interpretations for the same "visual information" being received through the eyes. We can say, then, that the picture is ambiguous because it can be interpreted in more than one way. This is the kind of challenge that your visual system faces. Just as the picture on the monitor has only two dimensions and so admits of more than one three-dimensional interpretation, so too, every time that you look at the world, the image projected on your retina has only two-dimensions and also can be interpreted as indicating the existence of more than one three-dimensional situation in the world.
If your visual system is going to avoid the threat of this kind of ambiguity and settle on not only a single interpretation, but hopefully (at least in most cases) the correct interpretation, then it must overcome what is called the inverse problem. In the case of vision, this problem can be stated as follows:
The Inverse Problem in Vision: The problem of retrieving all of the visual information about the 3D environment (the distal stimulus) using only the more limited information contained in the 2D image (the proximal stimulus) projected on the retina of the eye..
We do sometimes have experiences where our visual system has difficulty in overcomning the inverse problem and, thus, we are confronted with a visual scene that we experience as being ambiguous, with no single interpretation that is obviously superior to the alternatives. Consider the following example. At dusk, with the light diminishing, you look at a neighbor's house a block away and wonder why your neighbor's front door looks so dark. You know his door has always (at least in recent memory) been white. Does the doorway look dark because
- the door has been painted a dark color,
- the door is open and you are seeing the darkness of an unlighted house within, or
- the shadows are falling in an unusual way making the white door appear darker than it really is?
As you stare at the door, the image of the "dark door" reflected on your retina remains the same throughout. But your experience as you look at the door is likely to change subtley if your perspective shifts and you no longer see it as a door recently painted black but rather as a white door with unusual shadows falling on it.
These intriguing "shifts of perspective" (sometimes called "Gestalt switches") can be induced by ambiguous two dimensional line-drawing that confront us with an image that we can readily "see" in two quite different ways.
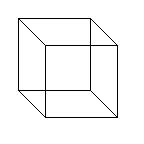 One
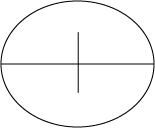
of the most famous is the Necker cube (figure at the right). Consider
the cube to be made of wire frame, with no walls. Which two-dimensional
square is closest to you? Is the top square closest and the bottom square
further away? Or is the bottom square closer? What happens when your
perspective shifts from one interpretation to the next? Does
the cube move?
One
of the most famous is the Necker cube (figure at the right). Consider
the cube to be made of wire frame, with no walls. Which two-dimensional
square is closest to you? Is the top square closest and the bottom square
further away? Or is the bottom square closer? What happens when your
perspective shifts from one interpretation to the next? Does
the cube move?
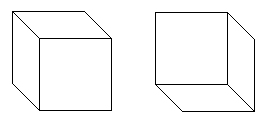 Cubes
can be drawn with solid walls, of course, which then resolves the ambiguity.
But there aren't always such obvious clues available in the real world.
Our visual system is required to resolve ambiguities that regularly
arise in the real world, and it must accomplish this feat on the basis
of information that seems, at least at first blush, to be insufficient
for the task. (There is actually some disagreement among researchers
in the field concerning how much hidden "information" there
is in most visual scenes to help remove this kind of ambiguity.)
Cubes
can be drawn with solid walls, of course, which then resolves the ambiguity.
But there aren't always such obvious clues available in the real world.
Our visual system is required to resolve ambiguities that regularly
arise in the real world, and it must accomplish this feat on the basis
of information that seems, at least at first blush, to be insufficient
for the task. (There is actually some disagreement among researchers
in the field concerning how much hidden "information" there
is in most visual scenes to help remove this kind of ambiguity.)
While we sometimes have visual experiences that are ambiguous, they are relatively infrequent. The surprising thing is that they don't happen more often. Given the inverse problem, one might expect that we would be plagued by ambiguity at every turn. How is it that our brain and visual system are so good at creating veridical experiences, that is, experiences that accurately represent the object(s) being perceived. It would seem that the relatively limited information coming in through the eye would simply not provide enough imformation. But somehow we do it. The queston is: How do we do it?
The sciences that study cognition and perception have made impressive progress over the past half-century in finding important clues that are helping us to answer the question: How do we do it? In the sections that follow, you will learn about some of those breakthroughs and about the theories that are now widely accepted. But there still remains a good deal that we do not fully understand, and there are some fascinating debates in the field between those who defend quite different theories of human vision. Before turning to the theories themselves, however, it is important to understand that there are a wide range of scientific methods employed in the study of vision and that this has important consequences. At this point, two basic issues are worth raising.
I. First, it is important to appreciate the fact that cognition and perception are so complex that no single research method has any reasonable hope of solving its mysteries. It is, thus, widely appreciated that the study of perception must be thoroughly interdisciplinary. It requires cooperation among researchers from different academic backgrounds and employing a diverse range of methodologies. This makes for an exciting and very dynamic research environment where, at any moment, a breakthrough in one field might have profound implications for reseach being done in another field. It also means that there are some experiments that can only be conducted properly with experts from a half-dozen fields
II. Second, there is a warning that must go with this multidisciplinary approach. There are times when more than one method can promise to offer a definitive answer to one and the same question. Sometimes it is possible to tell, even before the research is done, that one method will inevitably give a different answer to the question than will the other method (regardless of the specific outcome of the experiment). That is, it will sometimes be the case that the choice of research method will be far more important in determining the answer one receives than will any of the details derived from the research itself. Often, those involved in the research find their own methodology to be so "obviously" the correct one that they do not even bother to defend their choice of method. As you work through this study of perception, don't ever lose sight of the methods that are being employed and the supposed relevance of the "data" that is being acquired. Some of the most significant and far-reaching controversies in the cognitive sciences arise not because there is a disagreement about the data itself, but about the relevance of the data and the choice of methods that were used to acquire it. When there is a fundamental disagreement over proper methodology, it may be difficult (or impossible) to resolve the dispute without shifting to a philosophical debate about the fundamental presuppositions that one brings to the study in the first place -- presuppositions that may not be testable by any scientific experiment.
Let us turn, then, to a brief introduction to common methods employed in the study of perception in particular, and cognition in general.




